matematik
Türkçe matematik kelimesinin İngilizce karşılığı.n. mathematics, math, maths
Kısaca: Matematik, sayma, ölçme, cisimlerin şekillerini tanımlama gibi temel işlemlerden ortaya çıkan ve yapı, düzen ve ilişkileri inceleyen bilim dalı. Mantıksal irdeleme ve nicel hesaplamaları konu alan matematik, idealleştirme ve soyutlamalara dayanır. ...devamı ☟


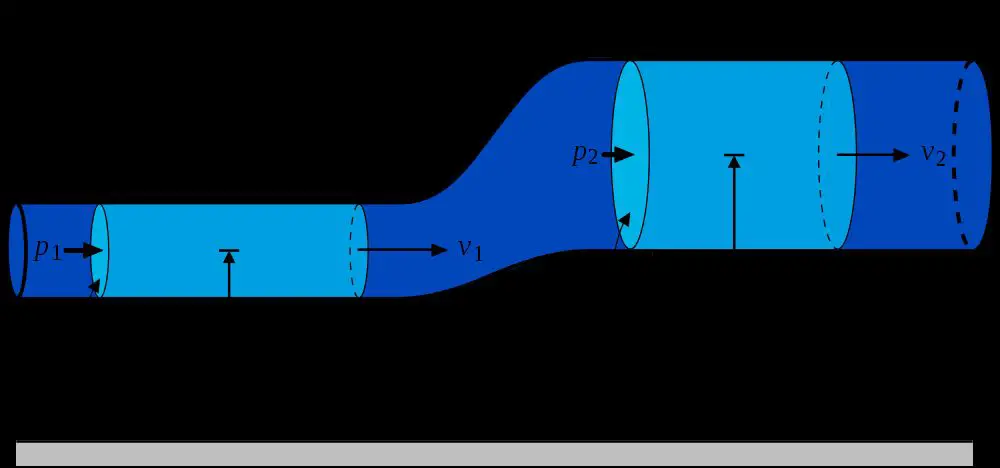

Matematik (Yunanca μάθημα máthēma, "bilgi, çalışma, öğrenme"), numaralar, felsefe, uzay ve fizik gibi konularla ilgilenir. Matematikçiler ve filozoflar...
Fermat, Analitik geometri, Analiz, Aritmetiğin Temel Teoremi, Cantor'un Diagonal Yöntemi, Cebirin Temel Teoremi, Dört Renk Teoremi, Eşyapı, Felsefe, Fermat'nın Son Teoremi, FizikMatematik felsefesi, matematiği anlama çabalarını sınıflandırmaya çalışan felsefe dalı. Başlıca soruları matematik ve matematiğin konusu olan nesnelerin...
Matematik felsefesi, Alfred Jules Ayer, Bertrand Russell, David Hilbert, Epistemoloji, Felsefe, Gottlob Frege, Kurt Gödel, Matematik, Matematiğin Temelleri, OntolojiMatematik mühendisliği. İyi derecede matematik bilgisine sahip, mühendislik eğitimi almış, endüstriyel problemleri modelleyerek çözebilen mühendisler yetiştirmeyi...
Yunan matematiği, Doğu Akdeniz kıyılarında MÖ 7. yüzyıldan MS 4. yüzyıla kadar uzanan dönemde yazılan matematik metinleri ile Klasik ve Helenistik dönemlerde...
Matematik Dünyası, Türk Matematik Derneği'nin sahibi olduğu lise ve üniversitelilere yönelik popüler matematik dergisidir. Yayın hayatına 1991'te ODTÜ'de...
Matematik Dünyası (dergi), Ali Nesin, Matematik, Taslakanlamda, soyut matematik, matematiğin soyut kavramlarını inceleyen bir kolu olarak adlandırılabilir. 18. yüzyıldan bu yana, soyut matematik matematiksel...
Tersine matematik, belirli bir teoremi ispatlamak için gerekli olan en az sayıdaki aksiyomların belirlenmesiyle ilgili matematik dalıdır. Çoğunlukla taban...
Tersine matematik, Matematik, Matematik Felsefesi, Matematiğin Temelleri, Taslak, İngilizce, Stephen George Simpson, Harvey FriedmanMatematik felsefesinde, sezgicilik ya da (eski sezgiciliğinin karşıtı olarak) yeni sezgicilik akımı, matematiğe insanların oluşturucu etkinliği olarak...
Sezgici Matematik, Doğal Sayılar, Küme, Kümeler Kuramı, Matematik, Matematik Felsefesi, Oluşturmacı Matematik, Rasyonel Sayılar, Taslak, Sezgici tip teorisi, Sezgici küme teorisi
misafir - 8 yıl önce
misafir - 7 yıl önce
misafir - 7 yıl önce
MSCNug - 3 yıl önce