Ayrık Olasılık Dağılımları
Kısaca: ayrık rassal değişken olarak bilinir. Bu halde ...devamı ☟
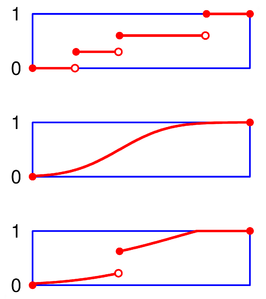
Olasılık teorisi
2 yıl önceolasılık teorisinin ana aksiyom sistemi olarak benimsenmiştir. Olasılık teorisine girişlerin çoğunda, ayrık olasılık dağılımları ve sürekli olasılık dağılımları...
Tekdüze dağılım (ayrık)
6 yıl önceAyrık tekdüze dağılım (İngilizce discrete uniform distribution), olasılık kuramı ve istatistik bilim kollarında, bir rassal değişken için belirli bir...
Olasılık dağılımı
2 yıl önceolasılık dağılımı olur. Bu dağılım ayrık olasılık dağılımıdır; çünkü sayılabilir şekilde ayrı ayrı sonuçlar ve bunlara bağlı olan pozitif olasılıklar...
Olasılık kütle fonksiyonu
2 yıl önceOlasılık kuramı bilim dalında bir olasılık kütle fonksiyonu bir ayrık rassal değişkenin olasılığının tıpatıp belli bir değere eşit olduğunu gösteren bir...
Sürekli olasılık dağılımları
2 yıl öncebaşarılır. Alternatif ve daha güçlü bir tanıma göre sürekli olasılık dağılımları terimi yalnızca olasılık yoğunluk fonksiyonu özelligine sahip olan dagilimlar...
Bernoulli dağılımı
2 yıl önce{\displaystyle q=1-p} olasılıkla başarısızlık ile 0 değeri alan bir ayrık olasılık dağılımıdır. İsmi ilk açıklamayı yapan İsviçreli bilim adamı Jakob Bernoulli...
Bernoulli dağılımı, Olasılık Dağılımları, İstatistik, Aralıklı olasılık dağılımı, Basıklık, Beklenen değer, Benford`un savı, Beta dağılımı, Binom dağılım, Binom dağılımı, Bozulmuş dağılımRademacher dağılımı
6 yıl önceBu dağılım sadece iki değeri olan bir ayrık rassal değişkenin, yani +1 ve -1 değerlerinin %50er şansla dağılmasını gösterir. Bu dağılım için olasılık kütle...
Rademacher dağılımı, Olasılık Dağılımları, Aralıklı olasılık dağılımı, Basıklık, Beklenen değer, Benford`un savı, Bernoulli dağılımı, Beta dağılımı, Binom dağılımı, Bozulmuş dağılım, Dirac delta fonksiyonuHipergeometrik dağılım
2 yıl öncearkasına n tane nesnenin çekilmesi işlemi için başarı sayısının dağılımını bir ayrık olasılık dağılımı şekilde betimler. Yaygın bir örnek, hatalı ve hatasız...
Hipergeometrik dağılım, Olasılık Dağılımları, Basıklık, Beklenen değer, Benford`un savı, Bernoulli dağılımı, Beta dağılımı, Binom dağılım, Binom dağılımı, Bozulmuş dağılım, Dirac delta fonksiyonu