fonksiyon
Türkçe fonksiyon kelimesinin İngilizce karşılığı.n. function
Kısaca: Bir nesnenin, bir şeyin ya da bir kişinin ait olduğu bütün ya da bir sistem içindeki kendine özgü faaliyeti. Bir şeyin, ait olduğu sınıfa özgü olan tarzda eylemde bulunma yetisi ya da gücü. Bir organın, parçaları birbirine bağımlı bir bütün içinde oynadığı kendisine özgü ve belirleyici, karakteristik rol. Bir şeyin kendisi özgü doğal eylemi. Aralarında bağımlılık ya da karşılıklılık ilişkisi bulunan düzenli nesne kümeleri arasındaki ilişkileri ifade eden kavram. ...devamı ☟
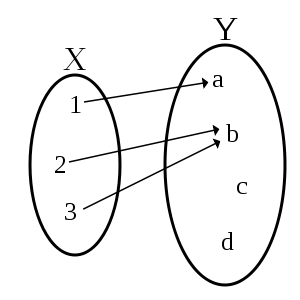


verilmiştir. Ama bir fonksiyon bir formül ya da bir kuraldan öte bir şeydir. Bir fonksiyon, sadece bir kural değildir; bir fonksiyonu tanımlamak için, kural...
İşlev (Matematik), Bağıntı, Bilgisayar bilimi, Biricik, Boolean, Fibonacci Serisi, Kalkış kümesi, Küme, Tanım kümesi, Yinelge, İçinesinüs fonksiyonunun faz açısı 0 dır. Ancak sinüs fonksiyonu sabit bir genlikli bir fonksiyon ile toplanmıştır (1). Bu sebepten, 0 anında fonksiyon toplam...
Meromorf fonksiyon, özellikle karmaşık analizde, bir fonksiyon çeşidi. Daha açık bir ifadeyle, meromorf fonksiyon, karmaşık düzlemin açık bir D kümesi...
Analitik fonksiyon, karmaşık düzlemde, açık kümeler üstüne tanımlı bir tür karmaşık değerli fonksiyon. Karmaşık düzlemin Ω (omega) ile gösterilen açık...
Analitik fonksiyon, Fonksiyon, KümeHolomorf fonksiyonlara bazen düzenli fonksiyonlar dendiği de olmaktadır. Karmaşık düzlemin tümünde holomorf olan fonksiyona tam fonksiyon adı verilir...
Gerçel fonksiyonlar, matematiksel analizin özellikle reel analizin klasikleşmiş nesneleridir.Bu bağlamda, gerçek değerli bir fonksiyonun aynı zamanda...
Gerçel fonksiyon, 1920, Fourier Analizi, Gerçek sayılar, Matematiksel analiz, Tanım kümesi, Fonksiyon analizi, Kompleks analiz, Karmaşık değişkenli fonksiyonlar, Kompleks fonksiyonlar, Görüntü kümesifonksiyonlar (tersanalitik fonksiyon veya antiholomorf de denilir) holomorf fonksiyonlara oldukça yakın ancak yine de onlardan ayrı olan fonksiyonlar...
Birim fonksiyon (özdeşlik fonksiyonu, özdeşlik gönderimi, özdeşlik dönüşümü, birim dönüşüm, birim işlev gibi farklı şekillerde de kullanılır), her zaman...
í–zdeşlik göndermesi, Matematik, Taslak, Varış kümesi, Görüntü kümesi, Gönderme