Türkçe Bilgi logo TürkçeBilgi

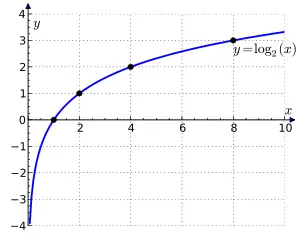
Logaritma

Kısaca: On yedinci yüzyılın başında hesapları hızlandırmak için yapılan bir buluş. 300 yıldan daha uzun bir zaman, temel bir hesap metodu olmuştur. On dokuzuncu yüzyılda masa hesap makinalarının doğuşu ve yirminci yüzyılda elektronik hesap makinalarının ortaya çıkışı, logaritmaya olan ihtiyacı azaltmıştır. ...devamı ☟

logaritma
Logaritma

On yedinci yüzyılın başında hesapları hızlandırmak için yapılan bir buluş. 300 yıldan daha uzun bir zaman, temel bir hesap metodu olmuştur. On dokuzuncu yüzyılda masa hesap makinalarının doğuşu ve yirminci yüzyılda elektronik hesap makinalarının ortaya çıkışı, logaritmaya olan ihtiyacı azaltmıştır. Ancak logaritmik fonksiyonların teorik ve uygulamalı matematikte özel bir yeri vardır.

Logaritma, birbirinden habersiz çalışan iki kişi tarafından keşfedilmiştir. Bunlar; 1614’te İskoçyalı John Napier ve 1620’de İsviçreli Joost Bürgi’dir.

Logaritma üzerinde önemli çalışmaları olan bir Türk bilgini de Gelenbevi İsmail Efendidir. Kendisi büyük matematikçi olup, mantıkla da uğraşmıştır. 1730-1790 yıllarında yaşayan bu büyük alimin Logaritma Risalesi isimli çok açık, anlaşılır yazılmış bir eseri mevcuttur.

Logaritmayı açıklamak için 2x2x2= 8 ifadesine bakalım. Bu 23= 8 olarak kısaca yazılabilir. Bu örnekte 3, 8’in 2 tabanına göre logaritması denir. Başka bir örnek, 2x2x2x2= 16 ve 24= 16 yazılırsa, burada 4, 16’nın 2 tabanına göre logaritmasıdır. Genel olarak bx= N ifadesinde N’nin b tabanına göre logaritması, x’tir. Her ne kadar her pozitif sayı taban olarak kullanılırsa da genel olarak logaritma 10 ve “e” (yaklaşık, 2,7182) tabanına göre hesaplanır.

Bayağı veya adi logaritma: Eğer logaritma 10 tabanına göre olursa, bu logaritma bayağı (adi) logaritma veya keşfeden Henry Briggs’e izafeten Briggs logaritma denir. Adi logaritma; 102= 100, 103= 1000, 104= 10000 eşitliklerine dayanır. bx= N genel denklemi 10x= N şekline, veya log10N= x haline gelir. Genelde buradaki 10 sayısı yazılmaz, sadece logN yazılır. Mesela; log150= 2,1761’dir. Buradaki 150 sayısı 100 ile 1000 yani 102 ile 103 arasında olduğundan logaritması 2 ile 3 arasındadır. Bu maksatla özel logaritma tabloları hazırlanmıştır.

Logaritma kullanılarak çarpmalar, toplamaya çevrilir. Mesela; 150 ile 254’ü çarpmak için, iki sayının logaritmaları tablodan bulunur ve toplanır. Sonra bu logaritmaya karşı gelen sayı tablodan aranır ki, bulunan sonuç, sözkonusu iki sayının çarpımından ibarettir. 150 ve 254’ün logaritmaları sıra ile 2,17661 ve 2,4048’dir. Toplam 4,5809 olur. Logaritması bu olan sayı aranırsa, 38100 bulunur.

Ancak logaritmanın tam kısmı, mesela 150’nin logaritması olan 2,1761’de 2, tablodan elde edilmez. Tablodan bunu takip eden sayılar okunur. 150 sayısının 100= 102 ile 1000= 103 arasında olduğu düşünülerek tamsayı kısmının 2 olduğu anlaşılır. Çarpma, logaritmaların toplam yapılarak elde edildiği gibi, bölme de, logaritmalar çıkarılarak elde edilir.

Tabii logaritma: Eğer taban olarak yaklaşık 2,71828 olan “e” sayısı alınırsa, bu logaritma tabii logaritma veya keşfeden John Napier’e izafeten Napier logaritması olarak da isimlendirilir. loge N yerine 1nN ifadesi kullanılır. Mesela, 1n2= 0,6932’dir. Tabii logaritma genel olarak, ilmi kanunların ifadesinde sık sık ortaya çıkar.

Adi ve tabii logaritmalar birbirleri ile alakalı olup, tabii logaritma, adi logaritmaya 0,4343 sayısı ile çarparak çevrilebilir.

Adi ve tabii logaritmaların dışında herhangi pozitif bir reel sayı tabanına göre de logaritma kullanılır. Ancak negatif sayıların hiçbir tabana göre logaritmasının olmayacağı açıktır.

logaritma

Büyük çarpmaları, bölmeleri, kök ve kuvvet alışlarını yapabilmek için bulunan bir yol; biri geometrik, öbürü aritmetik olarak kurulan iki sayı dizisinden aritmetik olanın her sayısı, karşılaştığı geometrik sayının logaritmasıdır:
"1 10 100 1000 10000 ... 0 1 2 3 4 ... dizilerinde 100 sayısının logaritmasının 2, 1000 sayısının ise 3 olduğu görülüyor."-

logaritma

Türkçe logaritma kelimesinin İngilizce karşılığı.
n. logarithm

logaritma

10 100 1000 10000 .... 0 1 23 4 .... dizilerinde 100 sayısının logaritmasının 2, 1000 sayısının ise 3 olduğu görülüyor.

logaritma

Türkçe logaritma kelimesinin Fransızca karşılığı.
logarithme [le]

logaritma

Türkçe logaritma kelimesinin Almanca karşılığı.
n. Logarithmus

İlgili konular

gelenbevi i̇smail efendi john napier reel sayı joost bürgi uygulamalı matematik

misafir - 8 yıl önce
teşekkürler ancak benim bilmek istedğim neden logaritmada negatif sayilar kullanilmiyor. ben bu konuda bilgi sahibi olmak istiyorum. yeterli bilgiye sahip olanlar mail atabilrmi? [email protected] kural o falan diye gelmeyin lütfen.

Görüş/mesaj gerekli.
Markdown kullanılabilir.

Logaritma
2 yıl önce

Logaritma, üstel işlevlerin tersi olan bir matematiksel işlevdir. Örneğin 1000'in 10 tabanına göre logaritması 3'tür çünkü 1000, 10'un 3. kuvvetidir,1000...

Logaritma, Gelenbevi İsmail Efendi, John Napier, Reel sayı, Joost Bürgi, Uygulamalı matematik
Adi logaritma
2 yıl önce

Adi logaritma (On tabanlı logaritma,Genel Logaritma) taban olarak 10 un kullanıldığı bir logaritma fonksiyonudur. Logaritmada her pozitif sayı taban olarak...
Ayrık Logaritma
6 yıl önce

Matematikte, özellikle soyut cebir ve uygulamalarında, ayrık logaritma, genel logaritmanın grup kuramındaki karşılığıdır. Genel olarak bakıldığında, loga(b)...
John Napier
2 yıl önce

Castle), Merchiston Baronu ve İskoçyalı bir matematikçi olan Napier, logaritmanın bulucusu olarak bilinir. Napier, Saint Andrews Üniversitesinde eğitim...

John Napier, 1550, 1617, 3 Nisan, Edinburgh, Logaritma, Matematikçi, Oxford Üniversitesi, İskoçya, Aritmetik dizi, Geometrik dizi
Matematiksel fonksiyonların listesi
2 yıl önce

benzerdir. Logaritmalar: üstel fonksiyonların tersleri; üstel denklemleri kapsayıp çözmek için faydalıdır. Doğal logaritma Adi logaritma İkili logaritma Belirsiz...
1614
2 yıl önce

John Naiper logaritma cetvelini buldu. 7 Nisan - Pocahontas ile John Rolfe evlendi.Powhatan adlı Kızılderili kabilesinin reisinin kızı, İngilizlere esir...

1614, 16. yüzyıl, 1609, 1610, 1611, 1612, 1613, 1615, 1616, 1617, 1618
Benford'un savı
6 yıl önce

genellikle logaritma olarak dağıldığı ve bunun bir sonucu olarak genel olarak pratik gerçek dünyada ölçme suretiyle ele geçen değerlerin logaritmalarının dağılımının...

Benford`un savı, Olasılık Dağılımları, Citation, MathWorld, Refend, Refbegin, 2007, Bernoulli dağılımı, Beta dağılımı, Binom dağılımı, Bozulmuş dağılım
Euler (anlam ayrımı)
6 yıl önce

bulduğu, Harmonik seri ile Doğal logaritma arasındaki limit bağıntısı. Euler sayısı - Euler'in bulduğu, doğal logaritmanın tabanı olan sabit(kısaca e {\displaystyle...