Türkçe Bilgi logo TürkçeBilgi

Cauchy Dağılımı

Kısaca: Cauchy-Lorentz dağılımı bir sürekli olasılık dağılımı olup, bu dağılımı ilk ortaya atan Augustin Cauchy ve Hendrik Lorentz anısına adlandırılmıştır. Matematik istatistikçiler genel olarak Cauchy dağılımı adını tercih edip kullanmaktadırlar; ama fizikçiler arasında Lorentz dağılımı veya bir Lorentz(yen) fonksiyonveya Breit-Wigner dağılımı olarak bilinip kullanılmaktadır. Fizik biliminde Cauchy-Lorentz dağılımının onemle kullanıldığı alanların bazıları şöyle anılabilir: Zorlanan rezonans fenomeni ...devamı ☟

Cauchy dağılımı
Cauchy Dağılımı

Cauchy-Lorentz dağılımı bir sürekli olasılık dağılımı olup, bu dağılımı ilk ortaya atan Augustin Cauchy ve Hendrik Lorentz anısına adlandırılmıştır. Matematik istatistikçiler genel olarak Cauchy dağılımı adını tercih edip kullanmaktadırlar; ama fizikçiler arasında Lorentz dağılımı veya bir Lorentz(yen) fonksiyonveya Breit-Wigner dağılımı olarak bilinip kullanılmaktadır. Fizik biliminde Cauchy-Lorentz dağılımının onemle kullanıldığı alanların bazıları şöyle anılabilir: Zorlanan rezonans fenomenini açıklayan deferensiyel eşitliğine çözüm sağlaması; spektroskopi alanında bir doğruşekil ile ayırım gösteren frekans aralığında aynı şekilde tüm atomlar birbirleriyle karşılıklı etkilemekteyken homojen genişlemeye tabi olamaları sonucu ortaya çıkan spektral doğrularının şeklinin tanımlanması; ve birçok mekanizmanın (özellikle çarpışmadan genişlemede) homojen genişleme göstermesinin açıklanması. Karakterizasyon

Olasılık yoğunluk fonksiyonu

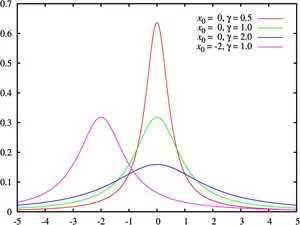
Cauchy dağılımı için olasılık yoğunluk fonksiyonu şudur: :\begin f(x; x_0,\gamma) &= \frac\right)^2\right]} \\[1] &= \left \right \end Burada x0 dağılımın doruğunu tanımlayan konum parametresi ve γ ise yarı-maksimumda yarı-genişliği tanımlayan ölçek parametresidir. Lorentziyen fonksiyonun genliği şöyle verilir: : \text = \frac Fizikte üç parametreli Lorentziyen fonksiyon çok kere şu türde verilir: :\begin f(x; x_0,\gamma,I) &= \frac\right)^2\right]} \\[2] &= \left \right \end Burada I doruktaki yüksekliktir. x0 = 0 ve γ = 1 olduğu zamanki özel hale standart Cauchy dağılımı adı verilir ve bunun olasılık yoğunluk fonksiyonu şöyle ifade edilir: : f(x; 0,1) = \frac. \!

Yığmalı dağılım fonksiyonu

Yığmalı dağılım fonksiyonu

şudur: :F(x; x_0,\gamma)=\frac \arctan\left(\frac\right)+\frac Cauchy dağılımı için ters yığmalı dağılım fonksiyonu şu olur: :F^(p; x_0,\gamma) = x_0 + \gamma\,\tan\left[3]. Özellikleri Cauchy dağılımı, tanımlanan hiçbir ortalaması, varyansı veya daha yüksek derecede momenti olmayan bir dağılıma örnektir. Mod değeri ve medyan değeri çok kesinlikle tanımlanmıştır ve her ikisi de x0a eşittirler. Eğer U ve V iki tane bağımsız 0 beklenen değerli ve 1e eşit varyanslı normal dağılım gösteren rassal değişkenlerse, U/V oranı standart Cauchy dağılımı gösterir. Eğer X1, … , Xn her biri bir standart Cauchy dağılımı gösteren bağımsız ama aynı dağılımlı rassal değişkenlerse, örneklem aritmetik ortalaması yani :(X1 + … + Xn)/n ifadesi de aynı dağılımı gösterir (Uçsal değerlerden etkilenmeyen örneklem medyani merkezsel konum ölçüsü olarak kullanılır.) Bunun doğru olduğunu isbatlamak için örneklem ortalamasının karakteristik fonksiyonu şöyle hesaplanabilir: :\phi_}(t) = \mathrm\left(e^\,t}\right) \,\! Burada \overline örneklem ortalamasıdır. Bu örneğin göstermektedir ki merkezsel limit teoremini daha basitleştirmek için kabul edilmesi gereken sonlu varyans hipotezinin bir kenara birakilması uygun değildir . Bu sonuç, aynı zamanda Cauchy dağılımının özel bir hali olduğu Levy çarpık alfa-durağan dağılımları için de geçerli olan merkezsel limit teoreminin alışılmış olandan daha genelleştirilmiş bir şekline bir örnek sağlamaktadır. Cauchy dağılımı bir sonsuza kadar bölünebilir olasılık dağılıma örnektir. Ayrıca kesinlikle dengelilik gösteren bir dağılımdir. Standart Cauchy dağılımı 1 serbestlik derecesi bulunan Student'in t-dağılımı ile aynidir. Cauchy dağılımının ait olduğu konum-ölçek ailesi tipte dağılımlara lineer kesirsel dönüşümler altında kapalı olma karekterini taşırlar.

Karakteristik fonksiyon

X Cauchy dağılım gösteren bir rassal değişken olsun. Cauchy dağılımı için karakteristik fonksiyon şöyle verilir: :\phi_x(t; x_0,\gamma) = \mathrm(e^) = \exp(i\,x_0\,t-\gamma\,|t|). \! Neden ortalama tanımlanmaz? Eğer bir olasılık dağılımı f(x) ile ifade edilen bir olasılık yoğunluk fonksiyonu gösteriyorsa, ortalama veya beklenen değeri şudur: :\int_^\infty x f(x)\,dx. \qquad\qquad (1)\! Burada sorun bunun şu ifade ile aynı olup olmadığıdır: :\int_0^\infty x f(x)\,dx-\int_^0 || f(x)\,dx.\qquad\qquad (2) \! Verilen (2) ifadesinin en çok bir terimi sonsuz ise bu iki ifade birbirine aynıdır. Fakat Cauchy dağılımı halinde (2) ifadesi için (sırayla pozitif ve negatif olan) her iki terim de sonsuzdur. Bu demektir ki (2) tanımlanamamaktadır. Ayrıca eğer (1) bir Lebesque entegrali olarak kabul edilirse, bu halde (1) de tanımlanamamaktdır; çünkü o zaman (1) ifadesinin (")nin pozitif ve negatif terimleri arasındaki fark olduğu görülür. Buna karşılık (1) ifadesi bir bir Lebesque entegrali olacak yerde bir has olmayan entegral olarak kabul edilirse, o halde (1)'in mutlaka her zaman iyi-tanımlanma karekteri bulunmayacaktır ama zaten (2) tanımlanamaktadır. O zaman (1) ifadesi şöyle yazilabilir: :\lim_\int_^a x f(x)\,dx, \! ve bu sıfıra eşit olan Cauchy ana değeridir. Fakat (1) ifadesi değişik şekilde şöyle de yazılabilir: :\lim_\int_^a x f(x)\,dx, \! Bu integral hesaplanınca açıkca görülür ki bu sıfır değerde değildir. Beklenen değer için olasılık kuramında ortaya çıkarılan çeşitli sonuçlar (örneğin güçlü büyük sayılar yasası), beklenen değeri bulunmayan Cauchy dağılımı için uygun olmamaktadır. Neden ikinci moment sonsuzdur? Ortalama anlamsiz oldugu icin bir standart Cauchy dagilimi icin varyans veya standart sapma kavramlari da anlamsizdir. Ancak ortalam etrafinda ikinic momentin ele alinmasi imkan dahilindedir. Su ifadeye gore :\mathrm(X^2) \propto \int_^ \,dx = \int_^ dx - \int_^ \,dx = \infty -\pi = \infty. \! gorulmektededir ki Cauchy dagilim icin ortalama etrafindaki ikinci moment sonsuzdur. İlişkili dağılımlar * İki bağımsız standart normal dağılım gösteren rassal değişşkenin birbirine oranı bir standart Cauchy dağılımı gösterir. Cauchy dağılımının bir oran dağılımı olduğu böylece açığa çıkar. * Standart Cauchy dağılımı, yani Cauchy(0,1) 1 serbestlik derecesi gösteren Student'in t dağılımına eşit olup Student'in t-dağılımınınn bir özel halidir. * Levy çarpık alfa-durağan dağılım ile ilişki şöyle verilir: Eğer X\sim \textrm\alpha\textrm(1,0,\gamma,\mu) ise, o halde X \sim \textrm(\mu,\gamma). olur. Relativistik Breit-Wigner dağılımı Nükleer fizikte ve parçacık fiziğinde, bir rezonansin enerji profili relativistik Breit-Wigner dağılımı ile belirtilir. Ayrıca bakınız * McCullagh's parametrization of the Cauchy distributions * Lévy uçusu ve Lévy süreci Dış bağlantılar * * [4] GNU Bilimsel Kütüphanesi - Referans El Kitabı.

Kaynaklar

Vikipedi

Bu konuda henüz görüş yok.
Görüş/mesaj gerekli.
Markdown kullanılabilir.

Olasılık dağılımı
2 yıl önce

Merkezsel olmayan t-dağılımı 2. tip Gumbel dağılımı Voigt dağılımı: Diğer bir adı Voigt profilidir. Bir normal dağılım ile bir Cauchy dağılımı konvolüsyonu sonucudur...
Student'in t dağılımı
2 yıl önce

bilim dallarında t-dağılımı ya da Student'in t dağılımı genel olarak örneklem sayısı veya sayıları küçük ise ve anakütle normal dağılım gösterdiği varsayılırsa...

Student`in t dağılımı, Olasılık Dağılımları, Basıklık, Beklenen değer, Benford`un savı, Bernoulli dağılımı, Beta dağılımı, Binom dağılımı, Bozulmuş dağılım, Dirac delta fonksiyonu, Dublin
Karakteristik fonksiyon
2 yıl önce

Cauchy dağılımı için karakteristik fonksiyon olduğu gözümlenebilir. Böylece Cauchy dağılımı için örneklem ortalaması için dağılım anakütle dağılımı ile...
Normal Dağılım
2 yıl önce

X/Y\sim \mathrm {Cauchy} (0,\sigma _{X}/\sigma _{Y})} şekilde Cauchy dağılımı gösterir. Böylece bu Cauchy dağılımı özel bir tip orantı dağılımı olur. Eğer X...

Normal Dağılım, Karl Friedrich Gauss, Rassal değişken, Yoğunluk fonksiyonu, Hipergeometrik dağılım, Pierre Simon Laplace, Abraham de Moivre
Zeta dağılımı
6 yıl önce

dağılımları şunlardır: Benford'un savı Cauchy dağılımı Lévy dağılımı Lévy çarpık alpha-durağan dağılımı Pareto dağılımı Zipf'in savı Zipf-Mandelbrot savı Allan...

Zeta dağılımı, Olasılık Dağılımları, Aralıklı olasılık dağılımı, Basıklık, Beklenen değer, Benford`un savı, Bernoulli dağılımı, Beta dağılımı, Binom dağılımı, Bozulmuş dağılım, Dirac delta fonksiyonu
Pareto Dağılımı
2 yıl önce

kullanılmıştır. İktisat bilim dalı dışında bu dağılım Bradford dağılımı adı altında da bilinmektedir. Pareto dağılımı iktisat dışında, sosyal bilimler, fen,...
Bernoulli dağılımı
2 yıl önce

ayrık olasılık dağılımıdır. İsmi ilk açıklamayı yapan İsviçreli bilim adamı Jakob Bernoulli anısına verilmiştir. Eğer X Bernoulli dağılımı gösteren bir...

Bernoulli dağılımı, Olasılık Dağılımları, İstatistik, Aralıklı olasılık dağılımı, Basıklık, Beklenen değer, Benford`un savı, Beta dağılımı, Binom dağılım, Binom dağılımı, Bozulmuş dağılım
Ki-kare dağılımı
2 yıl önce

dallarında ki-kare dağılım (x2 dağılımı) özellikle çıkarımsal istatistik analizde çok geniş bir pratik kullanım alanı bulmuştur. Bu dağılım, gamma dağılımından...

Ki-kare dağılımı, Matematik, Taslak