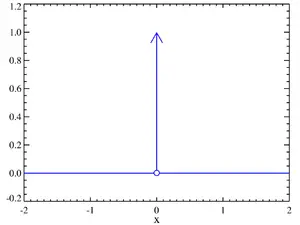
Dirac Delta Fonksiyonu

Kısaca: Adını Paul Dirac' tan alan Dirac delta fonksiyonu tek boyutta ...devamı ☟

Adını Paul Dirac` tan alan Dirac delta fonksiyonu tek boyutta

\delta(x-x_0) = \begin 
\infty, & x=x_0 \\ 0, & x \neq x_0 \end

şeklinde tanımlıdır. Bu gösterime uyacak bütün matematik temsillerine delta fonksiyonu veya delta fonksiyonunun temsili denir. Delta fonksiyonu n boyuta genellenebilir. Gösterimi ise

\delta^n(\vec x-\vec x_0)

şeklinde olur. Burada x ve x₀ n boyutlu vektörlerdir. Diğer taraftan n boyutta delta fonksiyonu her bir boyuttaki delta fonksiyonlarının çarpımı şeklinde de yazılabilir. Örneğin 3 boyutta

\delta^3(\vec x-\vec x_0)=\delta(x-x_0)\delta(y-y_0)\delta(z-z_0)

Dirac-Delta fonksiyonu basamak fonksiyonunun türevidir.

\delta (x)=\frac

Delta fonksiyonunun bazı özellikleri:

$\int_^\infty f(x)\delta(x-x_0)dx=f(x_0)$
$\delta(kx)=\frac\delta(x)$
$\delta(u(x))=\sum_i\frac$ burada $x_i$ , u(x) fonksiyonunun kökleridir.

Bazı delta temsilleri:

$\delta(x)= \lim_ \frac$
$\delta(x)= \lim_ \frace^{4\sigma^2$
$\delta(x)= \lim_ \frac\sin\left (\frac\right)$

Bu temsillerin normalizasyon katsayıları kontür integrali alınarak bulunabilir.

\frac\oint_\delta(z)dz=1

başlangıç noktaları ve genlikleri aynı ancak frekansları farklı sonsuz sayıda sinüsoidalin maksimum genlikleri tek bir noktada üst üste gelir ya da çakışır, bu nokta dirac fonksiyonunun kendisidir.

Kaynaklar

Vikipedi

İlgili konular

basamak fonksiyonu paul dirac vektör

Bu konuda henüz görüş yok.

Paul Dirac

2 yıl önce

ve kendi adı verilen Dirac denklemi'ni yaratmıştır. Dirac 1933 Nobel Fizik Ödülü'nü Erwin Schrödinger ile paylaşmıştır. Paul Dirac İngiltere'nin Bristol...

Matematiksel fonksiyonların listesi

2 yıl önce

Ackermann fonksiyonu: hesaplama teorisinde, bir hesaplanabilir fonksiyon, ilkel yinelemeli değildir. Böttcher fonksiyonu Dirac delta fonksiyonu: sıfır dışında...

Olasılık yoğunluk fonksiyonu

2 yıl önce

dallarında bir rassal değişken X için olasılık yoğunluk fonksiyonu bir reel sayılı sürekli fonksiyonu olup f ile ifade edilir ve şu özellikleri olması gereklidir:...

Bozulmuş dağılım

6 yıl önce

0 , x < c . {\displaystyle F(x)={\begin{cases}1,&x\geq c,\\0,&x<c.\end{cases}}} F(x) fonksiyonu bir basamaklı fonksiyon olur. Dirac delta fonksiyonu...

Green Fonksiyonları

4 yıl önce

herhangi bir çözümüdür burada δ {\displaystyle \delta } Dirac delta fonksiyonu'dur.Green fonksiyonunun bu özelliği form diferansiyel denklemleri...

Parçacık bozunması

6 yıl önce

{d^{3}{\vec {p}}_{i}}{(2\pi )^{3}2E_{i}}}\right)\,} denkleminden türetilebilir. burada δ 4 {\displaystyle \delta ^{4}\,} dört boyutlu Dirac delta fonksiyonudur....

Dalga Fonksiyonu

2 yıl önce

Kantum fiziğinde dalga fonksiyonu izole bir kuantum sistemindeki kuantum durumunu betimler. Dalga fonksiyonu karmaşık değerli bir olasılık genliğidir...

Dalga fonksiyonu, Paul Dirac, Schrödinger Denklemi, Werner Heisenberg, Matris mekaniği

Skellam dağılımı

2 yıl önce

{\displaystyle f(k;\mu )={\mu ^{k} \over k!}e^{-\mu }\,} Skellam olasılık kütle fonksiyonu iki Poisson dağılım arasındaki çapraz korelasyon olur (Skellam, 1946)...

Dirac Delta Fonksiyonu