Türkçe Bilgi logo TürkçeBilgi

Gauss Fonksiyonu

Kısaca: Gauss fonksiyonu (Carl Friedrich Gauss'tan sonra adlandırıldı), bir fonksiyon biçimidir ve şöyle ifade edilir: ...devamı ☟

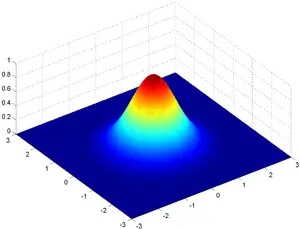
Gauss fonksiyonu
Gauss Fonksiyonu

Gauss fonksiyonu (Carl Friedrich Gauss'tan sonra adlandırıldı), bir fonksiyon biçimidir ve şöyle ifade edilir: :f(x) = a e^ } } Bazı reel sabitler için; a, b, c ve e ≈ 2,71828...(Euler sayısı). Gauss fonksiyonları, istatistikte normal dağılım tanımlamak için sıkça kullanılır. Ayrıca sinyal işlemede, Gauss filtresini tanımlamak; görüntü işlemede, iki boyutlu Gauss fonksiyonlarındaki Gauss bulanıklığında; matematikte, ısı denklemi ve difüzyon denklemini çözmek ve Weierstrass dönüşümünü tanımlamak için kullanılır. Özellikleri Gauss fonksiyonlarına üstel fonksiyon uygulanarak genel dördüncü derece fonksiyon elde edilir Gauss fonksiyonları, logaritmanın dördüncü dereceden fonksiyonlarıdır. Gauss fonksiyonları analitik ve limitleri x→∞ giderken0'dır. Gauss fonksiyonları ilkel fonksiyonu olmayan temel fonksiyondur. Gauss fonksiyonunun integrali hata fonksiyonudur. Tüm reel sayılardaki hata fonksiyonları, aşağıdaki Gauss integrali kullanılarak hesaplanabilir: :\int_^\infty e^\,dx=\sqrt Bu integral aşağıdaki biçime dönüştürülebilir: :\int_^\infty a e^ }\,dx=ac\cdot\sqrt. Burada, yalnızca a=1/(c√(2π)) için integral 1'dir. Bu durumda Gauss integrali, μ=b beklenen değeri ve σ2=c2 varyansına sahip normal dağıtılmış bir rassal değişkenin olasılık yoğunluk fonksiyonu olur, şöyle ki: : g(x) = \frac} e^\left(\frac\right)^2 }. Gauss fonksiyonları Fourier dönüşümündeki belirsizlik ilkesine göre sıfıra en yakın alanda bulunurlar. İki boyutlu Gauss fonksiyonu İki boyutta Gauss fonksiyonundaki e'nin kuvveti arttırıldığında fonksiyon dördüncü derece biçime dönüştürülür. Sonuçta Gauss fonksiyonu daima elips şeklindedir.

İki boyutlu Gauss fonksiyonu

na özel bir örnek şöyle verilebilir: :f(x,y) = A \exp\left(- \left(\frac + \frac \right)\right). Burada A katsayısı genlik; xo,yo merkez ve σx, σy, kabarcığın x ve y yayılımlarıdır. Buradaki şekil, A = 1, xo = 0, yo = 0, σx = σy = 1 kullanılarak elde edildi. Genellikle, iki boyutlu eliptik Gauss fonksiyonu şöyle ifade edilir: :f(x,y) = A \exp\left(- \left(a(x - x_o)^2 + 2b(x-x_o)(y-y_o) + c(y-y_o)^2 \right)\right) Bunun matris şöyledir: :\left a & b \\ b & c \end\right Bu matris "pozitif tanımlı matris" olarak adlandırılır. Bu formülasyonda A = 1, (xo, yo) = (0, 0), a = c = 1/2, b = 0 kullanılarak buradaki şekil elde edilir.

Genel denklem için parametrelerin anlamı

Denklemin genel biçimi için A katsayısı, tepenin yüksekliği ve (xo,yo), damlacığın merkezidir. a, b ve c parametreler şöyle verilsin: :a = \frac + \frac :b = -\frac + \frac :c = \frac + \frac Bu durumda damlacık saat yönünde \theta açıyla döndürülür (saat yönünün tersine döndürmek için b katsayısının işaretleri yer değiştirilir). Böylece şekil şöyle olur: Aşağıdaki Octave kodu kullanılarak parametrelerin değişim etkisi kolayca görülebilir: A = 1; x0 = 0; y0 = 0; sigma_x = 1; sigma_y = 2; for theta = 0:pi/100:pi a = cos(theta)^2/2/sigma_x^2 + sin(theta)^2/2/sigma_y^2; b = -sin(2*theta)/4/sigma_x^2 + sin(2*theta)/4/sigma_y^2 ; c = sin(theta)^2/2/sigma_x^2 + cos(theta)^2/2/sigma_y^2; Y = meshgrid(-5:.1:5, -5:.1:5); Z = A*exp( - (a*(X-x0).^2 + 2*b*(X-x0).*(Y-y0) + c*(Y-y0).^2)) ; surf(X,Y,Z);shading interp;view(-36,36);axis equal;drawnow end Çoğu fonksiyonlar, görüntü işleme ve gözün görme sistemi fonksiyonunun modellemesini hesaplamak için sıkça kullanılır.

Çok boyutlu Gauss fonksiyonu

n boyutlu bir uzayda Gauss fonksiyonu şöyle ifade edilir: : f(x) = \exp(-x^TAx) \;, Burada, x=\, n koordinatlarının sütunu;, A, bir "pozitif tanımlı n\times n matrisi" ve ^T, matrisin transpozesini (veya devriğini) ifade eder. Bir Gauss fonksiyonunun integrali tüm n boyutlu uzayda şöyle ifade edilir: : \int_^n}\exp(-x^TBx)dx = \sqrt}} \;. Biraz daha genelleştirme yapılırsa Gauss fonksiyonu şöyle olur: : f(x) = \exp(-x^TAx+s^Tx) \;, Burada s=\, kaydırma vektörüdür ve A matrisi A^T=A biçiminde simetrik kabul edilebilir. Bu fonksiyona ait aşağıdaki integraller aynı yöntemle hesaplanabilir: : \int d^nx e^ = \sqrt}} \exp(\fracv^TB^v)\equiv \mathcal\;. : \int d^n x e^ \left( a^T x \right) = (a^T u) \cdot \mathcal\;,\; \; u = \frac B^ v \;. : \int d^n x e^ \left( x^T D x \right) = \left( u^T D u + \frac (D B^) \right) \cdot \mathcal\;. : \begin & \int d^n x e^ \left( - \frac \Lambda \frac \right) e^ = \\ & = \left( 2 (A' \Lambda A B^) + 4 u^T A' \Lambda A u - 2 u^T (A' \Lambda s + A \Lambda s') + s'^T \Lambda s \right) \cdot \mathcal\;, \\ & \; u = \frac B^ v, v = s + s', B = A + A' \;. \end

Kaynaklar

Vikipedi

Bu konuda henüz görüş yok.
Görüş/mesaj gerekli.
Markdown kullanılabilir.

Gauss ışını
6 yıl önce

Gauss ışını optik biliminde, enine elektrik alanı ve yoğunluk dağılımı Gauss fonksiyonu ile tanımlanmış elektromanyetik ışın olarak tarif edilir. Birçok...
Carl Friedrich Gauss
2 yıl önce

matematiksel fonksiyonu, türev ve integralle ilgili temel teoremleri, normal dağılımı, Eliptik integrallerin ilk çözümlerini ve yüzeylerde Gauss eğimini keşfetmiş...

Matematik, Fizik, Geometri, Astronomi, Almanya, 1777, 1855, 23 Şubat, 30 Nisan, ABD, Adrien-Marie Legendre, Aksiyom, Alexander von Humboldt, Alman, Almanca
Gauss sabiti
6 yıl önce

{\begin{matrix}{\frac {1}{2}}\end{matrix}})} burada β beta fonksiyonu'dur. Gama fonksiyonu, Gauss sabitinin kapalı formu olarak kullanılırsa değişkene 1/4...
Normal Dağılım
2 yıl önce

bulunmamasıdır. Normal dağılım için sürekli olasılık yoğunluk fonksiyonu şu Gauss-tipi fonksiyondur: φ μ , σ 2 ( x ) = 1 σ 2 π e − ( x − μ ) 2 2 σ 2 = 1 σ φ...

Normal Dağılım, Karl Friedrich Gauss, Rassal değişken, Yoğunluk fonksiyonu, Hipergeometrik dağılım, Pierre Simon Laplace, Abraham de Moivre
Gauss integrali
2 yıl önce

dağılımın hem hata fonksiyonu hem de birikimli dağılım fonksiyonu ile yakından ilişkilidir. Hata fonksiyonu için her ne kadar temel fonksiyon olmazsa bile,...
Hipergeometrik fonksiyon
2 yıl önce

;x)=_{2}F_{1}(\alpha ,\beta ;\gamma ;x)} olup, bu fonksiyon Gauss hipergeometrik fonksiyonu veya hipergeometrik fonksiyon olarak bilinir. p F q ( a 1 , … , a p ;...
Gama fonksiyonu
2 yıl önce

Sanal kısım Bir alternatif gösterimde Gauss tarafından girilmişti. ve bazen Pi fonksiyonu deniyor,gama fonksiyonu terimleri yardımıyla Π ( z ) = Γ ( z...

Gama fonksiyonu, Faktöriyel, Fonksiyon, Karmaşık sayılar, Matematik, Reel sayı, Tam sayılar, Taslak
Olasılık dağılımı
2 yıl önce

yoğunluk fonksiyonu bulunmakta yani reel sayılar üzerinde bir negatif olmayan Lebesgue integrali bulunan şu f {\displaystyle f} fonksiyonu F ( x ) =...