Türkçe Bilgi logo TürkçeBilgi

Log-Normal Dağılım

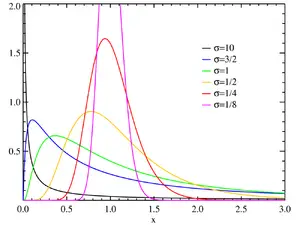
Kısaca: log-normal dağılım logaritması normal dağılım gösteren herhangi bir rassal değişken için tek-kuyruklu bir olasılık dağılımdır. Eğer ''Y'' normal dağılım gösteren bir rassal değişken ise, bu halde ''X'' exp(''Y'') için olasılık dağılımı bir log-normal dağılımdır; aynı şekilde eğer ''X'' log-normal dağılım gösterirse o halde log(''X'') normal dağılım gösterir. Logaritma fonksiyonu için bazın ne olduğu önemli değildir: Herhangi iki pozitif sayı olan ''a'', ''b'' ≠ 1 için eğer l ...devamı ☟

Log-normal dağılım
Log-normal Dağılım

log-normal dağılım logaritması normal dağılım gösteren herhangi bir rassal değişken için tek-kuyruklu bir olasılık dağılımdır. Eğer Y normal dağılım gösteren bir rassal değişken ise, bu halde Xexp(Y) için olasılık dağılımı bir log-normal dağılımdır; aynı şekilde eğer X log-normal dağılım gösterirse o halde log(X) normal dağılım gösterir. Logaritma fonksiyonu için bazın ne olduğu önemli değildir: Herhangi iki pozitif sayı olan a,b≠1 için eğer loga(X) normal dağılım gösterirse, logb(X) fonksiyonu da normaldir. Karekterizasyon

Olasılık yoğunluk fonksiyonu

Log-normal dağılım için olasılık yoğunluk fonksiyonu x>0 için şudur: : f(x;\mu,\sigma) = \frac}e^} Burada μ ve σ degiskenin logaritma degerleri icin ortalama ve standart sapmasidir. Bu halde parametreler kullanılan logaritma türünde (ya e bazlı, 2 bazlı veya 10 bazlı) birimlerdedir. Ancak radyo komunikasyon incelemelerinde bu parametreler tipik olarak desibel birimleri iledir.

Yığmalı dağılım fonksiyonu

Log-normal dağılım için yığmalı dağılım fonksiyonu şudur: :\frac+\frac \mathrm\left[1]

Momentler

Bütün momentler şu ifadelerle verilmiştir: :\mu_k=e^.

Moment üreten fonksyon

Log-normal dağılım için moment ureten fonksiyon bulunmamaktadır. == Özellikler Ortalama ve standart sapma Beklenen değer (ortalama) şudur: :\mathrm(X) = e^\,\! Varyans şöyle ifade edilir: :\mathrm(X) = (e^ - 1) e^\,\! ve standart sapma şu olur: :\mathrm(X) = \sqrt(X)} = \sqrt - 1)} e^\,\! Beklenen değer ve varyans verilmiş olduğu halde μ ve σ2 değerlerini elde etmek için kullanılan bağlantılar şöyle ifade edilir: :\mu = \ln(\mathrm(X))-\frac\ln\left(1+\frac(X)}(X))^2}\right)\,\! :\sigma^2 = \ln\left(\frac(X)}(X))^2}+1\right)\,\!

Mod ve medyan

Bu dağılım için mod şudur: :\mathrm(X) = e^\,\! Medyan şudur: :\tilde = e^\,\!

Geometrik ortalama ve geometrik standart sapma

Log-normal dağılım için geometrik ortalama e^\,\! ve geometrik standart sapma e^\,\! olur. Eğer bir örneklem veri serisi log-normal dağılım gösteren bir anakütleden gelmişse, geometrik ortalama ve geometrik standart sapma güvenlilik aralık kestirimi elde etmek için kullanılabilir. Bu noramal dağılım gösteren anakütleden gelen örneklem verilerinden aritmetik ortalama ve standart sapma kullanilarak güvenlilik aralığı bulmaya benzemektedir. / \sigma_\mathrm^3\,\! |- |2σ alt sınır |\mu - 2\sigma\,\! |\mu_\mathrm / \sigma_\mathrm^2\,\! |- |1σ alt sınır |\mu - \sigma\,\! |\mu_\mathrm / \sigma_\mathrm\,\! |- |1σ üst sınır |\mu + \sigma\,\! |\mu_\mathrm \sigma_\mathrm\,\! |- |2σ üst sınır |\mu + 2\sigma\,\! |\mu_\mathrm \sigma_\mathrm^2\,\! |- |3σ üst sınır |\mu + 3\sigma\,\! |\mu_\mathrm \sigma_\mathrm^3\,\! |} Burada geometrik ortalama \mu_\mathrm = \exp(\mu)\,\! ve geometrik standart sapma \sigma_\mathrm = \exp(\sigma)\,\! olur.

Momentler

Bu dağılım için ilk birkaç ham momentler şunlardır: :\mu_1=e^\,\! :\mu_2=e^\,\! :\mu_3=e^\,\! :\mu_4=e^\,\! :\mu_k=e^\,\!

Kısmi bekleyişler

== Parametrelerin maksimum olabilirlilik kestirimi == == İlişkili dağılımlar == * Eğer X \sim N(\mu, \sigma^2) bir normal dağılım gösterirse, o halde \exp(X) \sim \operatorname(\mu, \sigma^2). * Eğer X_m \sim \operatorname (\mu_m,\sigma_m^2), \ m= \ bağımsız olarak parametreleri aynı μ ve değişik σ olan log-normal dağılım gösteren değişkenlerse ve Y = \prod_^n X_m ise, o halde Y de log-normal dağılım gösteren değişkendir; yani Y \sim \operatorname \left( n\mu, \sum _^n \sigma_m^2 \right) olur. == Ayrıca bakınız == * Normal dağılım * Geometrik ortalama * Geometrik standart sapma * Hata fonksiyonu * Aitchison, J. and Brown, J.A.C. (1957), The Lognormal Distribution, * Brooks,R., Corson,J., ve Wales,J.D, (1994), "The Pricing of Index Options When the Underlying Assets All Follow a Lognormal Diffusion", Advances in Futures and Options Research, C7 * Hull, J. (2005), "Properties of Lognormal Distribution" Options, Futures, and Other Derivatives 6ed' * Lee,C.F. ve Lee, J. C. (to appear) "Normal and Lognormal Distribution" Alternative Option Pricing Models: Theory, Methods, and Applications, Kluwer Academic Publishers * Limpert,M., Stahel,W. ve Abbt,M., (2001) "Log-normal Distributions across the Sciences: Keys and Clues", BioScience, C.51 No.5 say. 341-352 * Swamee,P.K. (2002), "Near Lognormal Distribution", Journal of Hydrologic Engineering, C7 No.6 say.441-444 * Weisstein, E.W. et al. (2006) "Log Normal Distribution" 26 Ekim 2006.

Kaynaklar

Vikipedi

Bu konuda henüz görüş yok.
Görüş/mesaj gerekli.
Markdown kullanılabilir.

Normal Dağılım
2 yıl önce

Normal dağılım, aynı zamanda Gauss dağılımı veya Gauss tipi dağılım olarak isimlendirilen, birçok alanda pratik uygulaması olan, çok önemli bir sürekli...

Normal Dağılım, Karl Friedrich Gauss, Rassal değişken, Yoğunluk fonksiyonu, Hipergeometrik dağılım, Pierre Simon Laplace, Abraham de Moivre
Matris normal dağılım
6 yıl önce

dalları içinde matris normal dağılımı tek değişebilirli normal dağılımının çok değişkenli olarak genelleştirilmesidir. Matris normal dağılım gösteren çoklu rassal...
Olasılık dağılımı
2 yıl önce

dağılımı Katlanmış normal dağılımı Yarı-normal dağılımı Ters Gauss tipi dağılım: Wald dağılımı olarak da bilinir. Lévy dağılımı Log-logistik dağılımı...
Çokdeğişirli normal dağılım
2 yıl önce

çokdeğişirli normal dağılım veya çokdeğişirli Gauss-tipi dağılım, tek değişirli bir dağılım olan normal dağılımın (veya Gauss-tipi dağılımın) çoklu değişirli...
Logistik dağılım
2 yıl önce

olan normal dağılıma çok benzer; fakat kuyrukları daha ağır olduğu için daha basık bir şekil gösterir. Logistik dağılım ismini yığmalı dağılım fonksiyonuna...

Logistik dağılım, Olasılık Dağılımları, Basıklık, Beklenen değer, Benford`un savı, Bernoulli dağılımı, Beta dağılımı, Binom dağılımı, Bozulmuş dağılım, Dirac delta fonksiyonu, F-dağılımı
Üstel dağılım
2 yıl önce

üstel dağılım olan Exp(λ0) ile ('yaklaşık' dağılım) olan Exp(λ) arasında yönlendirilmiş Kullback-Leibler ayrılımı şöyle verilir: Δ ( λ | | λ 0 ) = log ⁡ (...

Üstel dağılım, Olasılık Dağılımları, Basıklık, Bağımsızlık, Beklenen değer, Benford`un savı, Bernoulli dağılımı, Beta dağılımı, Binom dağılımı, Bozulmuş dağılım, Dirac delta fonksiyonu
Ki-kare dağılımı
2 yıl önce

ki-kare dağılım (x2 dağılımı) özellikle çıkarımsal istatistik analizde çok geniş bir pratik kullanım alanı bulmuştur. Bu dağılım, gamma dağılımından elde...

Ki-kare dağılımı, Matematik, Taslak
Mod
2 yıl önce

elde edilir. Y rassal değişkenin logaritması normal dağılım gösterir ve bu nedenle Y dağılımına log-normal adı verilir. Özel bir X seçilerek ortalaması...