polinom
Türkçe polinom kelimesinin İngilizce karşılığı.n. polynomial
Polinom
Kısaca: Polinom (fr. polynome). Mat. Polinom fonksiyon, bir cisim veya değişli bir halka içinde, bu cisim veya halkadaki bir x elemanının, oransal ve tam bir ifade ile tanımlanan f uygulaması. Biçimsel polinom, bir cisim veya daha genel olarak değişli bir halka içinde belirli bir sıradan başlayarak hepsi sıfır olan terimler dizisi; işlemler bu dizilerin üzerinden tanımlanır. ...devamı ☟
a0, a1, a2, ...an reel sayı, x değişken ve n de doğal sayı olmak üzere;
a0xn +a1xn-1+a2xn-2+ ...+an-1x+ an
şeklindeki ifade. Polinomlar P (x), Q (x), ile gösterilir.
Bu kısaca [1] şeklinde gösterilebilir, a0, a1, a2, … nicelikleri P polinomunun katsayılarıdır, her katsayının indisi, kendi sırasının bir büyüğüne eşittir. Sıfır olmayan bir tek an katsayısı vardır ve bundan sonra gelenlerin hepsi sıfırdır; n'ye P'nin derecesi denir. İki polinom aynı sıradan alınmış aynı katsayılardan meydana gelmişse birbirine eşittir. Bir tek katsayı sıfırdan farklı ise, polinom bir birterimli olur. iki polinomun toplamı aynı sıradaki katsayıları toplanarak elde edilir; toplam polinomun derecesi, en çok bu iki polinomdan birinin derecesine eşit olur; bir halka veya bir cisim üzerindeki polinomların cümlesi toplama için değişli bir gruptur; etkisiz elemanın (sıfır polinom) bütün katsayıları sıfırdır.
Bir polinomu bir skalerle çarpmak için, katsayılardan her biri bu skalerle çarpılır: X [2] = [3]. Bir cisim veya bir tamlık halkası için, XP çarpımının derecesi P'nin derecesine eşittir. Tamlık halkası olmayan bir halka için, bu derece P'ninkinden küçük olabilir; gerçekten, “Kan çarpımı, çarpanlardan hiç biri sıfır olmasa da sıfır olabilir. Bir cismin üzerindeki polinomlar cümlesi vektör uzayı yapısına sahiptir; sıfır olmayan ai ve bj katsayılı iki birterimlinin çarpımı, ai bj katsayıları sıfır olmayan, i + j dereceden bir birterimlidir. iki [4] ve [5] polinomunun çarpımı, ok katsayısının değeri €ai bj olan bir polinomdur; toplam i + j = k bağıntısını veren katsayılar üzerinden alınmıştır. Çarpımın derecesi en çok iki polinomun dereceleri toplamına eşit olur. Bir cisim veya bir tamlık halkası söz konusu ise, çarpımın derecesi yine iki polinomun dereceleri toplamına eşittir. Bir A halkası üzerindeki polinomların cümlesi de bir halka, yani A üzerindeki polinomlar halkasıdır. Bir K cismi içinde, X= (0,1,0,-0,…) polinomu göz önüne alınırsa
X2 = (0,0,1,0), X3 = (0,0,0,1,0…) v.b. elde edilir ve P = (ao. aı, … an, 0,0, …) polinomu P = ao X° + aı X1 + a2 X2 + … + anXn şeklinde yazılabilir. X'e, K cismi üzerinde alınmış sayısal bir değer verilirse, P bir polinom fonksiyonu gösterir. R gerçek sayılar cismi ve C karmaşık sayılar cismi içinde, x'in her değeri için, aynı sayısal değeri alan iki polinom özdeştir; bunların indirgenemez polinomların çarpımı halinde ayrılışı ancak bir şekilde mümkündür; C cismi halinde, bu işlemden d'Alembert teoremi çıkar: n'inci dereceden bir polinomun n kökü vardır. Fakat bu özellik genelleştirilemez: mesela, modülo p uygunluklarının Z/p cismi içinde (p asal bir sayı olmak üzere) farklı iki polinom, değişkenin bütün değerleri için aynı sayısal değeri alabilir. Çok değişkenli polinomlar hali, katsayılarında birçok indis bulunan biçimsel polinomlar yardımıyle incelenir.
n. polynomial
Bu konuda henüz görüş yok.
polinom Resimleri
Polinom
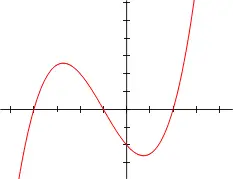
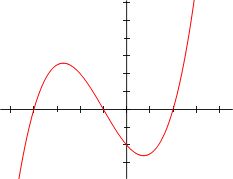
3 yıl öncebir polinom olan x2 − 4x + 7, ikinci dereceden bir polinomdur. Diğer bir örnek olarak, x2 − 4/x + 7x3/2 bir polinom değildir, çünkü polinomlarda terimlerin...
Polinom, Cebirin Temel Teoremi, Fonksiyon, Niels Henrik AbelPolinom bölme
3 yıl önceCebirde polinom bölme, bir polinomu, eşit ya da daha düşük dereceli bir polinoma bölme algoritmasıdır. Uzun bölme olarak adlandırılan aritmetik yöntemin...
Cebirsel Geometri
3 yıl öncebir polinom denklem sistemini sağlıyor ise, bir cebirsel eğri üzerindedir denir. Klasik cebirsel geometrinin ilgilendiği temel nesneler, polinomların bir...
P ile NP arasındaki ilişki
7 yıl öncepolynomial" ifadelerini temsil eder, Türkçe karşılıkları "polinom" ve "belirleyici olmayan polinom"dur. "P eşittir NP?" ise hesaplama teorisi'nin en temel...
P ile NP arasındaki ilişki, Asal Sayılar, NP-complete, NP (karmaşıklık), P (karmaşıklık), Polinomsal zamanda çalışan algoritma, Üstel zamanda çalışan algoritma, Hesaplama TeorisiDoğrusal fonksiyon
3 yıl öncedallarında doğrusal fonksiyon, derecesi sıfır veya bir olan polinom fonksiyon veya sıfır polinomdur. Doğrusal cebir ve fonksiyonel analizde doğrusal fonksiyon...
Döngüsel artıklık denetimi
3 yıl önceperformansa göre CRC polinomunu tasarlanır. En büyük yanılgı, "en iyi" CRC polinomlarının ya indirgenemez polinom ya da indirgenemez polinomların 1 + x faktörü...
Cebirin Temel Teoremi
3 yıl önceb^{2}-4ac<0} koşulunu sağlayan polinomlar). Sabit olmayan, gerçel katsayılara sahip her polinom, derecesi 1 veya 2 olan polinomların çarpımı şeklinde yazılabilir...
Cebirin Temel Teoremi, Karmaşık sayılar, Matematik, Polinom, TaslakMatematiksel fonksiyonların listesi
3 yıl önceQuintic fonksiyon: Beşinci derece polinom. Sextic fonksiyon: Altıncı derece polinom. Rasyonel fonksiyonlar: İki polinomun oranıdır. n. kök Kare kök: Sonuçları...