Euler Bağıntısı
Bu bağıntıyla iki matematiksel ifade olan i ve birbirine bağlanmış oldu, bu açıdan çok önemli bir ifadedir.
de Moivre Eşitliği
Euler bağıntısından da rahatlıkla görülebileceği gibi tümevarımla da ispatlanabilen bir eşitliktir.
Kısaca: Dönüşüm formülleri trigonometride kullanılan, toplam durumundaki iki trigonometrik ifadeyi çarpım haline getirmeye yarar. ...devamı ☟
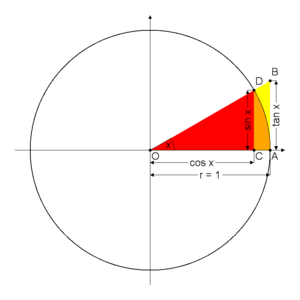
bölümüyle hesaplanır. cos A = | A B | | A C | {\displaystyle \cos A={\frac {|AB|}{|AC|}}} Sinüs Tanjant Kotanjant Dönüşüm formülleri Yarım açı formülleri...
Kosinüs, Açı, Dönüşüm formülleri, Hipotenüs, Matematik, Sinüs, Tanjant, Taslak, Trigonometri, Yarıçap, ÇemberA = cos A sin A {\displaystyle \cot A={\frac {|AB|}{|BC|}}={\frac {1}{\tan A}}={\frac {\cos A}{\sin A}}} Kosinüs Sinüs Tanjant Dönüşüm formülleri...
Kotanjant, Dik üçgen, Matematik, Taslak, Ordinat, Birim çemberA = | B C | | A B | = sin A cos A {\displaystyle \tan A={\frac {|BC|}{|AB|}}={\frac {\sin A}{\cos A}}} Kosinüs Sinüs Kotanjant Dönüşüm formülleri...
Tanjant, Fonksiyon, Geometri, Orijin, Taslak, TrigonometrikMatematikte ters trigonometrik fonksiyonlar, tanım kümesinde bulunan trigonometrik fonksiyonların ters fonksiyonudur. arcsin, arccos, arctan sırasıyla...
önemli sonucun daha zarif bir şekilde formüle edilebilmesine olanak verir. En dikkat çekici olan şudur ki trigonometrik fonksiyonlar içeren analizlerin sonuçları...
Radyan, Daire, Matematik, Taslak, Yarıçapve verimlilik avantajları sağlayabilir. Kosinüs Tanjant Kotanjant Dönüşüm formülleri ^ Uta C. Merzbach, Carl B. Boyer (2011), A History of Mathematics...
bağlı olarak, bir doğrusal dönüşüm hataların normal dağılım göstermesine sonuç olabilir. Bu nedenle bir doğrusal dönüşüm kullanmayı seçmek için modelin...
θ {\displaystyle y=r\sin \theta \,} Bu iki formüle göre x ve y cinsinden elde edilen dönüşüm formülleri ise şöyledir: r = x 2 + y 2 {\displaystyle r={\sqrt...
Kutupsal koordinat sistemi, Kutupsal koordinat sistemi, 1625, 1647, 1816, Akışkan, Antik Yunan uygarlığı, Arşimet, Açı, Açısal momentum, Blaise Pascal