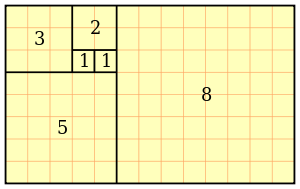
F_n := F(n):=
\begin
0 & \mbox n = 0; \ 1 & \mbox n = 1; \ F(n-1)+F(n-2) & \mbox n > 1. \ \end
Fibonacci sayılarının ilginç özellikleri vardır. Mesela n sayısı büyüdükçe iki ardışık Fibonacci sayısının oranı Altın oran`a yani 1.618... e yakınsar.
Ayrıca bakınız : Fibonacci sayıları