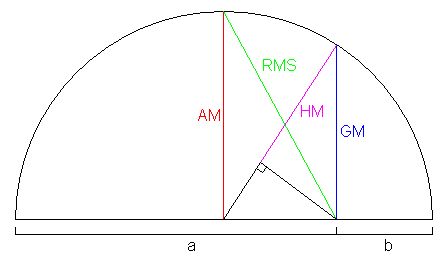
Genelleştirilmiş Ortalama

genelleştirilmiş ortalama Pisagorik ortalamalarını, yani aritmetik ortalama, geometrik ortalama ve harmonik ortalamayı, ayni tanınım formülünde birleşetirip kapsayan bir abstre genelleştirmedir. Güç ortalaması veya Holder ortalaması adları da verilmektedir. Tanınım Eğer

p

sıfır olmayan bir pozitif reel sayı ise, $p$ üslü genelleştirilmiş ortalama :

M_p(x_1,\dots,x_n) = \left( \frac \cdot \sum_^n x_^p \right)^.

ifadesine uyan

x_1,\dots,x_n

pozitif reel sayılardır. Özellikler

t

= 1 hali aritmetik ortalama,

t

= - 1 harmonik ortalamasını ve t = 2 ise ortalama kare kökünü ortaya çıkartır. t limitte 0a yaklaşırsa, M(t') için verilen sayılar için limit o sayıların geometrik ortalamasını verir ve bu nedenle M(0) terimini geometrik ortalama olarak tanımlamak uygun olur. Bunun yanında t ∞ değerine limitte yaklaşmakta ise, M(t) verilen sayıların minimum değerine yaklaşım gösterir. * Birçok değişik ortalamalar gibi, genelleştirilmiş ortalama,

x_1,\dots,x_n

argumanlarının bir homojen fonksiyonudur. Yani

b

pozitif bir reel sayı ise,

b\cdot x_1,\dots, b\cdot x_n

reel sayılarının

p

üslü genelleştirilmiş ortalaması

b

teriminin

x_1,\dots, x_n

sayılarının genelleştirilmiş ortalamasına eşittir. * Yarı-aritmetik ortalamalar için uygulandığı gibi, ortalamanın hesaplanması birbirine eşit büyüklükte alt-blokların hesaplanması ile elde edilebilir. ::

M_p(x_1,\dots,x_) =  M_p(M_p(x_1,\dots,x_),  M_p(x_,\dots,x_),  \dots,  M_p(x_,\dots,x_))

Genelleştirilmiş ortalama eşitsizliği

Genellikle, eger

p < q

olursa, o halde

M_p(x_1,\dots,x_n) \le M_q(x_1,\dots,x_n)

olur ve iki ortalama ancak ve ancak

x_1 = x_2 = \cdots = x_n

ise birbirine eşittir. Bundan şu sonuç ortaya çıkartılır: :

\forall p\in\mathbb\ \frac\geq 0,

ve bu Jensen'in eşitsizliğini kullanılarak isbat edilebilir. Özellikle,

p\in\

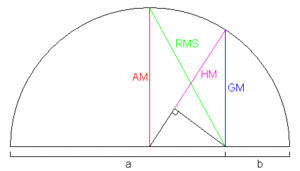
ise genelleştirilmiş ortalama eşitsizliği hem Pisagorik ortalamaların eşitsizliğini hem de aritmetik ve geometrik ortalamaların eşitsizliğini içermektedir. Özel haller *

\lim_ M_p(x_1,\dots,x_n) = \min \

- minimum, *

M_(x_1,\dots,x_n) = \frac+\dots+\frac}

- harmonik ortalama, *

\lim_ M_p(x_1,\dots,x_n) = \sqrt [1]

- geometrik ortalama, *

M_1(x_1,\dots,x_n) = \frac

- aritmetik ortalama, *

M_2(x_1,\dots,x_n) = \sqrt}

- kuadratik ortalama, *

\lim_ M_p(x_1,\dots,x_n) = \max \

- maksimum. Kuvvet ortalamaları eşitsizliğinin isbatı

Karşıt işaretli ortalamalar arasındaki eşitsizlerin birbirine tıpatıp benzemesi

p ve q endeksli güç ortalamaları arasında bir ortalama bulunsun: :

\sqrt [2]^nw_ix_i^p}\leq \sqrt [3]^nw_ix_i^q}

O halde: :

^n\frac}

(Bu pozitif reel sayılı kesinlikle azalan bir fonksiyon olduğu icin) iki tarafın da -1 üssü alınabilir: :

\sqrt [6]^nw_ix_i^}=\sqrt [7]^nw_i\frac}}\geq \sqrt [8]^nw_i\frac}}=\sqrt [9]^nw_ix_i^}

Böylece -p ve -q üsleri olan ortalamalar için bir eşitsizlik elde etmiş oluruz. Aynı mantığı tersden de kullanabilip eşitsizliklerin birbirine aynı olduğu isbat edilebilir. (Bu sonuç ileri de kullanılacaktır.)

Geometrik ortalama

Herhangi bir q değeri için, q üslü bir ortalama ile geometrik ortalama arasındaki eşitsizliğin şu yolla dönüşümü yapılabilir: :

\prod_^nx_i^ \leq \sqrt [10]^nw_ix_i^q}

^nw_ix_i^q}\leq \prod_^nx_i^

(Birinci eşitsizlik bir pozitif q için isbat edilmiş olması gerekir.) Her iki tarafdan q üssü alınırsa :

\prod_^nx_i^ \leq \sum_^nw_ix_i^q

olur. Her iki halde de

x_i^q

silsilesi için ağırlıklı aritmetik ve geometrik ortalamalar arasındaki eşitsizlik ele geçirilir. Bu Jensen'in eşitsizliği ve logaritmik fonksiyonun konkav olduğu gerçeklerinden faydalanarak isbat edilebilir. :

\sum_^nw_i\log(x_i) \leq \log(\sum_^nw_ix_i)

\log(\prod_^nx_i^) \leq \log(\sum_^nw_ix_i)

(Kesinlikle azalan) exp fonksiyonu her iki tarafa tatbik edilirse, şu eşitsizlik ortaya çıkar: :

\prod_^nx_i^ \leq \sum_^nw_ix_i

Böylece, herhangi bir pozitif q değeri için şu ifade önerilir: :

\sqrt [12]^nw_ix_i^}\leq \prod_^nx_i^ \leq \sqrt [13]^nw_ix_i^q}

Bu eşitsizlik herhangi bir q ne kadar küçük olursa olsun hep gerçek olacağı için, q limitte 0a yaklaştıkca, bu eşitsizliğin sol ve sağ tarafları geometrik ortalamaya yaklaşıklık gösterir. q 0a yaklaşım gösterdikce, güç ortalaması limitte geometrik ortalamaya yaklaşır: :

^nw_ix_i^}=\prod_^nx_i^

Herhangi bir güç ortalamaları çifti arasındaki eşitsizlik

Burada herhangi bir p<q için şu eşitsizliğin geçerli olduğu isbat edilecektir: :

\sqrt [15]^nw_ix_i^p}\leq \sqrt [16]^nw_ix_i^q}

* Eğer p negatif ise ve q pozitif ise, eşitsizlik yukarıda isbatı verilenin aynıdır: :

\sqrt [17]^nw_ix_i^p}\leq \prod_^nx_i^ \leq\sqrt [18]^nw_ix_i^q}

* Hem p pozitif hem de q pozitif ise isbat şöyle yapılır: Önce şu fonksiyon tanımlanır: :

f:\rightarrow,

f(x)=x^}

. Burada f bir güç fonksiyonudur; bu nedenle ikinci türevi bulunup şöyle ifade edilir: :

f

(x)=(\frac)(\frac-1)x^-2}, Bu f sahası içinde kesinlikle pozitif olur; çünkü q > p olduğu için f konvekstir. Bu sonucu ve Jensen'in eşitsizliğini kullarak, şu ifadeler elde edilir: : $f(\sum_^nw_ix_i^p)\leq\sum_^nw_if(x_i^p)$ : $^nw_ix_i^p}\leq\sum_^nw_ix_i^q$ Bunun her iki tarafının 1/q üssü alınırsa (1/q)'nin pozitif olması nedeniyle bunun bir artan fonskiyon görülür ve elde edilen eşitsizlik şu olur: : $\sqrt [20]^nw_ix_i^p}\leq\sqrt [21]^nw_ix_i^q}$ Bu eşitsizlik ise isbat gereken sonucdur. * Hem p negatif ve hem q negatif ise, daha önce gösterilenlere aynı olan ifadeler geçerlidir ve bunlara -p ve -q konulursa, isbatı istenilen eşitsizlik yine elde edilir.
Minimum ve maksimum

Minimum ve maksimum
değerlerin üssel endeksleri : $-\infty$ ve $+\infty$ . olan güç ortalamaları olduğu kabul edilsin. Böylece herhangi bir q değeri için : $^nw_ix_i^q}\leq \max (x_1,x_2,\ldots ,x_n)$ Maksimum için isbat şöyle yapılır: Genelliği kaybetmeden x_i dizisinin artan olmadığını ve ağırlığının sıfır olduğu kabul edilsin. Bu halde eşitsizlik şu ifadeyle aynıdır: : $^nw_ix_i^q}\leq x_1$ Bu ifadenin iki tarafının da q üssü alınırsa, (qnun işaretine bağlı olarak) şu iki ifadeden birisi elde edilir: : $\sum_^nw_ix_i^q\leq \geq} x_1^q$ ≤ eger q>0 , ≥ eger q<0. Her iki taraftan $w_1x_1$ çıkartılırsa, elde edilen ifade : $\sum_^nw_ix_i^q\leq \geq} (1-w_1)x_1^q$ olur. Bu $(1-w_1)$ ile bölünürse, ortaya çıkan ifade şudur: : $\sum_^n\fracx_i^q\leq \geq} x_1^q$ 1 - w₁ sıfır değildir, böylece : $\sum_^n\frac=1$ İki taraftan x₁q çıkartırsak ortaya çıkan ifade : $\sum_^n\frac(x_i^q-x_1^q)\leq \geq} 0$ olur. Bu epeyce açıkca anlaşılır; çünkü x₁ herhangi bir x_i değerine eşit veya o değerden daha fazladır ve böylece : $x_i^q-x_1^q\leq \geq} 0$ Minimum için de isbat nerede ise aynı şekilde yapılır; ancak x₁, w₁ yerine x_n, w_n kullanılır. Genelleştirilmiş $f$ -ortalaması 'Genelleştirilmiş ortalama (veya güç ortalaması') daha da genelleştirilip genelleştirilmiş f-ortalaması formülü ortaya çıkarılmıştır. Bu formül şöyledir: : $M_f(x_1,\dots,x_n) = f^ \left(\cdot\sum_^n}\right)$ Bu formüle göre güç ortalaması $f\left(x\right)=x^p$ olarak elde edilir. Uygulamalar
Sinyal üretilmesi
Bir güç ortalaması bir doğrusal olmayan hareketli ortalama hizmeti görür. Bu küçük $p$ için düşük sinyal değerlerine doğru kaydırma yapar ve büyük $p$ için yüksek sinyal değerlerine önem sağlar. Hareketli aritmetik ortalamanın etkin uygulaması (yani smooth uygulaması) gerçekse verilen şu Haskell koduna göre powerSmooth :: Floating a => ([24] -> [25]) -> a -> [26] -> [27] powerSmooth smooth p = map (** recip p) . smooth . map (**p) * Bu büyük değerde $p$ için rektifiye edilmiş sinyal üzerinde bir zarf detektörü olarak hizmet görebilir. * Bu küçük değerde $p$ için kütle spektrumu üzerinde anahat detektörü olarak hizmet görebilir. Ayrıca bakınız * Aritmetik ortalama *
Geometrik ortalama
* Harmonik ortalama * Pisagorik ortalama * Ortalama * Ortalama kare kökü Dış bağlantılar * MathWorld'de güç ortalaması * Genelleştirilmiş ortalama için örnekler * PlanetMath sitesinde genelleştilmiş ortalama hakkında eşitsizlik ispatı * Rasyonel ortalama
Kaynaklar
Vikipedi

Genelleştirilmiş Ortalama

Genelleştirilmiş Ortalama Hakkında Detaylı Bilgi

Genelleştirilmiş ortalama eşitsizliği

Karşıt işaretli ortalamalar arasındaki eşitsizlerin birbirine tıpatıp benzemesi

Geometrik ortalama

Herhangi bir güç ortalamaları çifti arasındaki eşitsizlik

Minimum ve maksimum

Minimum ve maksimum

Sinyal üretilmesi

Geometrik ortalama

Kaynaklar

Görüşler ve Yorumlar

Genelleştirilmiş ortalama Resimleri