isim =zeta|
tip = kütle|
pdf_image =
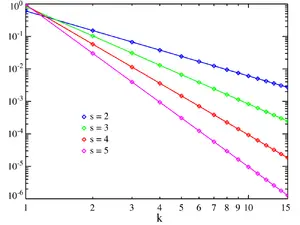
log-log ölcekli olarak Zeta OKF. (Bu fonksiyon sadece k`nin tamsayıları icin tanımlanmaktadır; noktaları bağlayan çizgiler görüs kolaylıgı sağlamak icin verilmistir; süreklilik ifade etmezler.)|
cdf_image =
|
parametreler =|
destek =|
OYF =|
YDF =|
ortalama =|
medyan =|
mod =|
varyans =|
çarpıklık =|
basıklık =|
entropi =|
mf =|
kf =|
Olasılık kuramı ve istatistik bilim kollarında, ``zeta dağılımı`` bir aralıklı olasılık dağılımıdır. Eğer ``X`` ``s`` parametresi ile zeta dağılımı gösteren bir bir rassal değişken ise, ``X``in ``k`` tamsayısı değerini almasının olasılığı şu olasılık kütle fonksiyonu ile belirtilir:
Burada ζ(``s``) Riemann zeta fonksiyonu olur (ama bu fonksiyon ``s`` = 1 tanımlanamaz.).
Sonsuz değerde ``N`` için zeta dağılımı Zipf dağılımı eşit değerdedir. O zaman ``Zipf dağılımı`` ve ``zeta dağılım`` aynı anlamı verdikleri için birbiriyle kavram farkı vermeden değiştirilebilip kullanılırlar.
Momentler
Genel olarak, ``n``inci ham moment ``X````n``in beklenen değeri olarak şöyle tanımlanır:Bu ifadenin sağ tarafında bulunan seri bir Rieman zeta funksiyonu temsil eden seridir. Ancak bu serinin yakınsaması sadece ``s-n`` değeri birden büyük ise mümkün olmaktadır. Böylece zeta dağılımı için moment
\begin \zeta(s-n)/\zeta(s) & \textrm~n < s-1 \\infty & \textrm~n \ge s-1 \end \right.
olur. Hatırlamak gerekir ki iki zeta fonksiyonunun oranı, ``n`` ≥ ``s`` − 1 ifadesi için bile, çok kesin olarak tanımlanmıştır. Ama bu yine de, momentlerin seri için tanımlandığı ve bu nedenle büyük bir ``n`` değeri için tanımlanamadığı gerçeğini değiştirmez`
Moment üreten fonksiyon
Genel olarak, moment üreten fonksiyon şöyle tanımlanır:
Bu seri gerçekte yalnızca bir polilogaritma`nin tanımlanmasıdır ve için geçerlidir ve bu halde
Bu fonksiyonun bir Taylor serisi yöntemi kullanılarak genişletilmesi mutlaka bir dağılım için momentleri vermez. Genellikle, moment üreten fonksiyonlara dayanarak elde edilen momentleri kullanan Taylor serileri şu ifedeyi ortaya çıkartır:
Bu ifade, büyük ``n`` değerleri icin momentlerin sonsuz olduğu gerçeği göz önüne getirilirse, besbellidir ki herhangi bir ``s``nin sonsuz olmayan değeri icin kesin olarak tanımlanamaz. Momentler yerine analitik olarak sürekli terimleri kullanırsak, polilogaritmayi temsil eden seriden
için şu ifadeyi elde ederiz:
değeri şöyle verilir
burada ``H````s`` bir harmonik sayı olur.
``s``=1 hali
harmonik seri olduğu için ζ(1) sonsuz değerdedir ve bu nedenle ``s``=1 olma hali anlamlı değildir. Ama eğer ``A`` yoğunluğu bulunan herhangi bir pozitif tamsayılar seti ise yanivar olmakta ise ve burada ``N``(``A``, ``n``) ``A`` seti içinde bulunan ve ``n`` değerine eşit veya bu değerden daha küçük set elemanlarının sayısı ise, şu ifade
bu yoğunluğa eşittir.
Bazı hallerde ``A`` için yoğunluk yok olması nedeniyle verilen ikinci sınır geçerli olur. Örnegin, eğer ``A`` birinci tamsayısı ;``d`` olan bütün pozitif tamsayıların bir seti ise, ``A`` için bir yoğunluk bulunmaz. Ancak bu halde bile yukarıda verilen ikinci sınırlama gecerli olur ve bu sınırlama şu ifadeye oranlıdır:
Buna benzer yöntem aynen Benford`un savının geliştirilmesi için de kullanılır.
İçsel kaynaklar
Diğer ``güç-savı`` dağılımları şunlardır:- Benford`un savı
- Cauchy dağılımı
- Lí©vy dağılımı
- Lí©vy çarpık alpha-durağan dağılımı
- Pareto dağılımı
- Zipf`in savı
- Zipf-Mandelbrot savı
Kaynak
- Kaynak wiki
Dışsal bağlantılar
`` Some remarks on the Riemann zeta distribution`` by Allan Gut. Gut`un “Reieman zeta dağılımı” olarak andıgı ``X`` bir rassal değisken olarak −log ``X``, ifadesinin dağılımıdır. Bu kavram genellikle ve bu maddede zeta dağılımı olarak anılmaktadır.Olasılık Dağılımları|Zeta dağılımı